Στα δύο προηγούμενα άρθρα αναφερθήκαμε στον Τζέιμες Γιουνγκ (Jaymes Young) και το τραγούδι του “Infinity (Άπειρο)”, καθώς και στον Θανάση Παπακωνσταντίνου και τους στίχους του τραγουδιού του «Επιτύμβιο», το οποίο επίσης αναφέρεται στο Άπειρο.
Η έμπνευσή τους προέρχεται και από την επιστήμη και την φιλοσοφία. Όπως ήδη αναφέραμε η γενική θεματική αυτών των άρθρων είναι το άπειρο και το πόσο έχει εμπνεύσει αυτή η δυσνόητη έννοια διάφορους καλλιτέχνες ή συγγραφείς.
Στο παρόν άρθρο θα αναφερθούμε στην ανάλυση που κάνει ο Αριστοτέλης στα «Φυσικά ή Φυσική Ακρόασις» για το Άπειρο. Ο Αριστοτέλης στο έργο του «Φυσικά» ασχολείται με την ανάλυση των βασικών αρχών που διέπουν την φύση, όπως οι έννοιες της κίνησης, του απείρου, του χώρου και του χρόνου.
Τα «Φυσικά», λόγω της ιδιαίτερης δυσκολίας που έχουν στην κατανόηση εννοιών της φυσικής δεν απετέλεσαν προτεραιότητα για τους κλασικιστές, εκτός από περιπτώσεις εξαιρετικών ξένων επιστημόνων, όπως ο W.D. Ross, αλλά και ελλήνων, όπως ο Βασίλης Κάλφας (εκδόσεις Νήσος) και ο Βασίλης Μπετσάκος (εκδόσεις Ζήτρος).
Έτσι, ακόμη και η μεγάλη βάση των αρχαιοελληνικών κειμένων «Περσέας (Perseus)» στο διαδίκτυο δεν τα περιλαμβάνει. Επίσης, υπάρχουν λίγες νεοελληνικές αποδόσεις των «Φυσικών» του Αριστοτέλη. Ίσως μαζί με τη έκδοση των «Φυσικών» από τον Κάκτο, το έργο των κ.κ. Κάλφα και Μπετσάκου, να είναι οι τρεις μοναδικές σύγχρονες (των τελευταίων τριών δεκαετιών) νεοελληνικές αποδόσεις του έργου αυτού.
Υπάρχουν και μερικές ακόμη εκδόσεις των «Φυσικών» (Πάπυρου, Γεωργιάδη, κ.λπ.), αλλά είναι παλαιότερες, δυσεύρετες και δεν έχουν την εμβάθυνση και τα ερμηνευτικά σχόλια, ιδιαίτερα του έργου των κ.κ. Κάλφα και Μπετσάκου..
Το έργο αυτό του Αριστοτέλη αποτελείται από οκτώ βιβλία. Στο τρίτο βιβλίο ο φιλόσοφος αναφέρεται στην κίνηση και το άπειρο. Θεωρεί σαν δεδομένο ότι η φυσική επιστήμη έχει ως ασχολία τα μεγέθη των σωμάτων, την κίνηση και τον χρόνο.
Σαν δεύτερο επίπεδο θεωρεί το εάν είναι άπειρα ή πεπερασμένα, αν και αφήνει περιθώριο για καταστάσεις που δεν ανήκουν σε καμία από τις δύο κατηγορίες. Έτσι, καταλήγει ότι θεωρεί σημαντικό να ασχοληθεί κάποιος με την θεωρία του απείρου, με πρώτο ερώτημα αν υπάρχει ή όχι και αν η απάντηση είναι θετική τότε να αναρωτηθεί τί είναι αυτό («καὶ εἰ ἔστιν, τί ἐστιν»).
Επομένως, συμπεραίνει ότι η θεωρία του απείρου ανήκει στην φυσική επιστήμη. Προσθέτει ότι για το άπειρο είχαν μιλήσει όλοι όσοι είχαν ασχοληθεί με την φυσική φιλοσοφία, θεωρώντας ότι ήταν μία κάποια αρχή των όντων.
Συνεχίζοντας γράφει ότι οι Πυθαγόρειοι και ο Πλάτων δέχονται ότι το άπειρο είναι μία αυθύπαρκτη ουσία και όχι μία τυχαία («συμβεβηκός») ιδιότητα κάποιου άλλου πράγματος. Επιπλέον, μόνο οι Πυθαγόρειοι τοποθετούν το άπειρο μεταξύ των αντικειμένων της αίσθησης (καθώς δεν θεωρούν τον αριθμό χωριστό από αυτά) και ισχυρίζονται ότι αυτό που βρίσκεται έξω από τον ουρανό είναι άπειρο («εἶναι τὸ ἔξω τοῦ οὐρανοῦ ἄπειρον»).
Ο Πλάτων, από την άλλη πλευρά, υποστηρίζει ότι δεν υπάρχει σώμα έξω από τον ουρανό (οι Ιδέες δεν είναι έξω γιατί δεν είναι πουθενά), ωστόσο δέχεται ότι το άπειρο είναι παρόν όχι μόνο στα αντικείμενα της αίσθησης, αλλά και στις Ιδέες («Πλάτων δὲ ἔξω μὲν οὐδὲν εἶναι σῶμα, οὐδὲ τὰς ἰδέας, διὰ τὸ μηδὲ ποὺ εἶναι αὐτάς, τὸ μέντοι ἄπειρον καὶ ἐν τοῖς αἰσθητοῖς καὶ ἐν ἐκείναις εἶναι»).
Επιπροσθέτως, οι Πυθαγόρειοι ταυτίζουν το άπειρο με το άρτιο. Γι’ αυτό, λένε, ότι όταν αποκόπτεται και κλείνεται από το περιττό, παρέχει στα πράγματα το στοιχείο του απείρου. Μια ένδειξη αυτού είναι αυτό που συμβαίνει με τους αριθμούς.
Στο σημείο αυτό ο Βασίλης Μπετσάκος αναγνωρίζει την ιδιαίτερη δυσκολία κατανόησης του κειμένου που ακολουθεί. Γράφει ο Αριστοτέλης ότι αν οι γνώμονες, το γεωμετρικό όργανο που μοιάζει με Γ σχηματίζοντας ορθή γωνία μεταξύ των δύο πλευρών του, τοποθετηθούν γύρω από το ένα, και χωρίς το ένα, στη μία κατασκευή το σχήμα που προκύπτει είναι πάντα διαφορετικό, στην άλλη είναι πάντα το ίδιο («περιτιθεμένων γὰρ τῶν γνωμόνων περὶ τὸ ἓν καὶ χωρὶς ὁτὲ μὲν ἄλλο ἀεὶ γίγνεσθαι τὸ εἶδος, ὁτὲ δὲ ἕν»).
Εδώ ο Αριστοτέλης αναφέρεται στα Πυθαγόρεια μαθηματικά και φιλοσοφία, διότι εάν ξεκινήσει κάποιος από το ένα και στη συνέχεια τοποθετήσει ένα γνώμονα γύρω από αυτό και μετά τοποθετήσει και άλλο γνώμονα το σχήμα που θα σχηματιστεί θα είναι τετράγωνο, το οποίο είναι συνδεδεμένο με το «περιττό».
Εάν σχηματίσουμε το πρώτο επίπεδο θα έχουμε το ένα και τρία πετραδάκια στις άκρες του γνώμονα και στην κορυφή της ορθής γωνίας, άρα σύνολο τέσσερα. Το τέσσερα είναι το τετράγωνο του δύο. Αν προσθέσουμε και δεύτερο γνώμονα και βάλουμε πέντε πετραδάκια (που είναι ο επόμενος περιττός αριθμός) θα έχουμε στο σύνολο εννέα πετραδάκια που είναι το τετράγωνο του τρία, κ.ο.κ. (Σχήμα 1).
Έτσι σχηματίζεται μία ωραία μαθηματική παράσταση η 1 + 3 + 5 + …+ [ 2 (ν – 1) ] = ν2. Το μαγικό σε αυτή την περίπτωση είναι ότι με αυτό τον τρόπο σχηματίζονται τετράγωνα των οποίων ο λόγος των πλευρών είναι πάντα ένα, εξ’ ου και ο Αριστοτέλης αναφέρει ότι το σχήμα είναι το ίδιο!
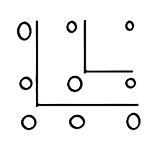
Στην δεύτερη περίπτωση με τους άρτιους αριθμούς το σχήμα που σχηματίζεται είναι ορθογώνιο και έχει πάντα διαφορετικό λόγο των πλευρών (Σχήμα 2).
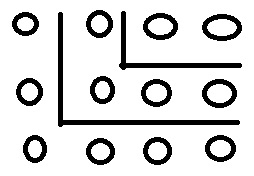
Έτσι, πιστεύω ότι ξεδιαλύνεται η δυσκολία του κειμένου, διότι στην μεν πρώτη περίπτωση των περιττών αριθμών έχουμε ένα σχήμα, το τετράγωνο, με ίδιο λόγο πλευρών το ένα (1), ενώ στην δεύτερη περίπτωση των περιττών αριθμών προκύπτουν άπειρα ορθογώνια, με διαφορετικό λόγο των πλευρών τους!
Ο Ross αναφέρει πολλές περιπτώσεις υπομνηματιστών των έργων του Αριστοτέλη, καθώς και νεότερων συγγραφέων, όπως του Sir Thomas Little Heath και του Zeller για το θέμα αυτό. Ο Αριστοτέλης συνεχίζει αναφέροντας ότι ο Πλάτωνας θεωρεί ότι υπάρχουν δύο άπειρα, το μεγάλο και το μικρό.
Άλλη μία σπαζοκεφαλιά εδώ. Τι εννοεί ο Πλάτωνας με το μεγάλο και το μικρό άπειρο; Προφανώς αυτό που συναντούν οι μαθηματικοί συνέχεια στα όρια, όταν μία μεταβλητή τείνει στο συν άπειρο ή το μείον άπειρο.
Η ουσία είναι μάλλον ότι με το μικρό άπειρο ο Πλάτων θεωρούσε ότι μπορούμε να τμήσουμε ένα αντικείμενο άπειρες φορές, κάτι που δεν συμβάδιζε με αυτό που πίστευε ο Δημόκριτος. Στο σημείο αυτό θα κλείσουμε το κείμενο αυτό συνοψίζοντας με το ότι οι απόψεις γύρω από το άπειρο είναι πάρα πολύ ενδιαφέρουσες για τους θετικούς επιστήμονες, αλλά και για τους φιλοσόφους.
Θα έλεγα ότι η ανάλυσή του απείρου συνδέεται με αρκετές άλλες έννοιες (περιττό – άρτιο) και μας οδηγεί ίσως σε μυστικιστικούς ατραπούς, κρίνοντας από την ερμηνεία των περιττών αριθμών σύμφωνα με τους Πυθαγόρειους. Να τονίσω ότι κατά τους Πυθαγόρειους το τετράγωνο με πλευρά δύο (2) ήταν συνδεδεμένο με την δικαιοσύνη (διότι κατά τον φυσικό νόμο μας επιστρέφεται ότι κάνουμε)!
Βασίλης Τσιάντος
Καθηγητής Διεθνούς Πανεπιστημίου της Ελλάδος
Πρόεδρος Δ.Ε. Παραρτήματος Καβάλας Ε.Μ.Ε.













